Mathematical method universal constants and important numbers: Part - I

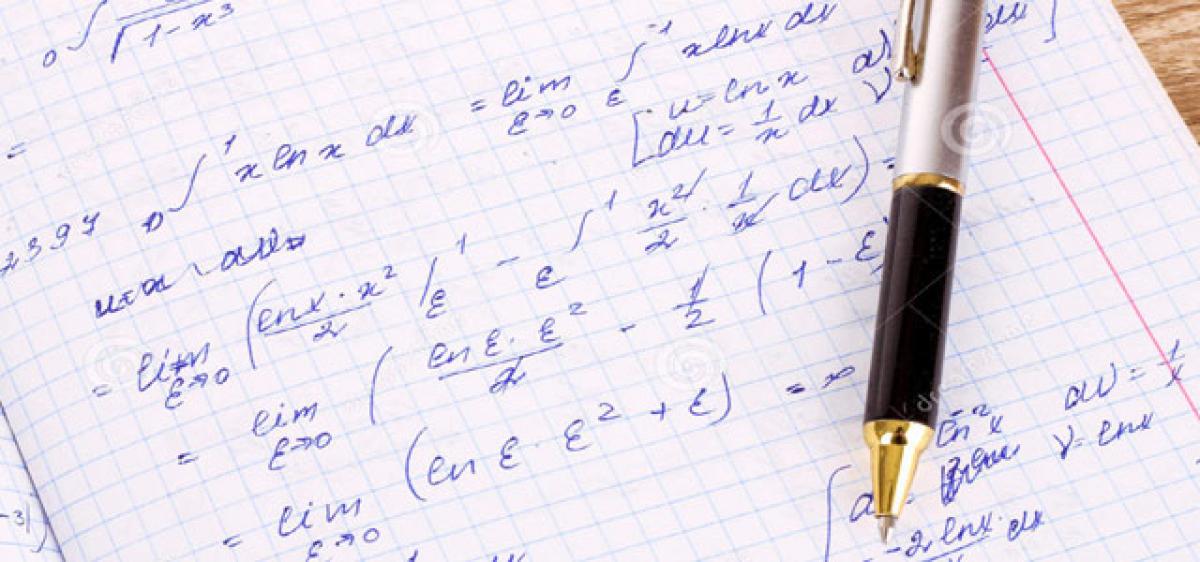
Before we commence the fascinating journey of discovering the beauty of certain mysterious numbers call the natural numbers I would like to introduce the readers to a few established mathematical methods of arriving at conclusions.

In mathematics, the sieve of Eratosthenes is a simple, ancient algorithm for finding all prime numbers up to any given limit.

Mathematical induction is a method of mathematical proof typically used to establish a given statement for all natural numbers. It is a form of direct proof, and it is done in two steps.

The first step, known as the base case, is to prove the given statement for the first natural number. Then it holds for the next number. It is therefore follows that if the statement is true for any number n, then it must be true for the next one too. In other words it is true for all natural numbers.

Iteration is the act of repeating a process, either to generate an unbounded sequence of outcomes, or with the aim of approaching a desired goal, target or result.

Each repetition of the process is also called” iteration and the results of one iteration are used as the starting point for the next iteration.

In the context of mathematics or computer science, iteration (along with the related technique of recursion) is a standard building block of algorithms.

The method of exhaustion, in mathematics, is a technique invented by the classical Greeks to prove propositions regarding the areas and volumes of geometric figures.

Although it was a forerunner of the integral calculus, the method of exhaustion used neither limits nor arguments about infinitesimal quantities.

It was instead a strictly logical procedure, based upon the axiom that a given quantity can be made smaller than another given quantity by successively halving it (a finite number of times).

From this axiom it can be shown, for example, that the area of a circle is proportional to the square of its radius.

“Counting – how it began”
Embedded deeply into the structure of the mysterious universe in which we live are many fascinating numbers.

There are many numbers to which mankind, in its anxiety to explain the phenomena that present themselves in the environment through a rational and scientific approach ascribes numbers. These "numbers" in reality, represent the true nature of the universe.

The very concept of numbers or "counting" began with a process called subitizing – meaning to know at a glance how much a small number of things amount to by looking at a bunch of convenient figures such as straight lines, to represent each of them, and making a mental approximation of how many lines there are.

In 1960 the Ishango bone, or the thigh - bone of a baboon, was discovered. 20,000 years old, it had grooves carved into it, representing sequences of numbers.

History has records to show that, on the other hand, piraha tribe, which exists even today in the Amazon rainforest, completely did away with the need to deal with numbers at all. Their language helped them decide how to communicate their requirements through a series of gestures.

It is only in very recent times, “recent” being used in the context of anthropological measurements of time, that mankind learnt the art of using the digits of the fingers of the hands and feet to count, essentially upto ten, and thereafter in multiples thereof.,

Even today it is not uncommon for people to communicate through gestures instead of numbers - such as the signs that stockbrokers make during bidding or the participants in an auction.